约瑟夫环

约瑟夫环问题是一个经典的数学问题，也称为约瑟夫问题。它描述的是这样一个场景：N个人围成一圈，从第一个人开始报数，报到M的人出列，然后从下一个人开始继续报数，如此循环，直到所有人都出列为止。这个问题可以用来模拟一些实际生活中的场景，比如军队中的排队点名、公司中的裁员等。

约瑟夫环问题可以用多种方法解决，包括递归、循环队列等。在计算机科学中，这个问题常用来考察编程能力，特别是在数据结构方面的应用。

如果您有关于约瑟夫环问题的具体问题或需要进一步的解释，请随时告诉我。

约瑟夫环问题：一个经典的数学与算法挑战

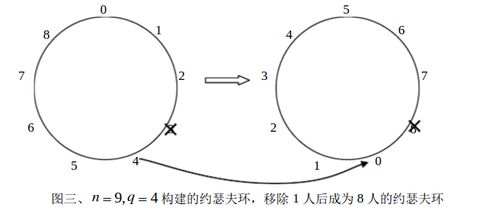
约瑟夫环问题是一个古老的数学问题，它不仅考验着我们的数学思维，也挑战着我们的编程能力。本文将深入探讨约瑟夫环问题的背景、解题思路以及多种算法实现。

一、问题的起源与背景

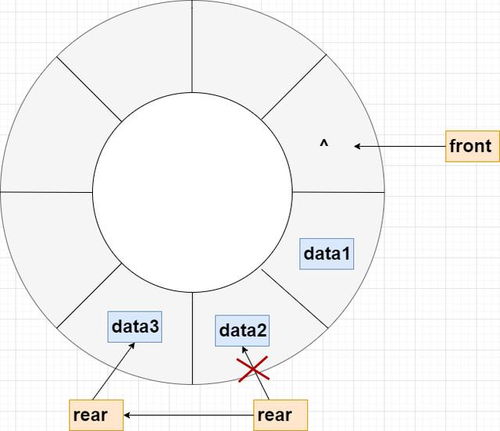
约瑟夫环问题最早可以追溯到古罗马时期，据说是一个关于犯人被围成一圈，每隔一定人数就淘汰一个人的故事。这个问题在数学和计算机科学领域有着广泛的应用，是许多算法设计的基础。

二、问题描述与目标

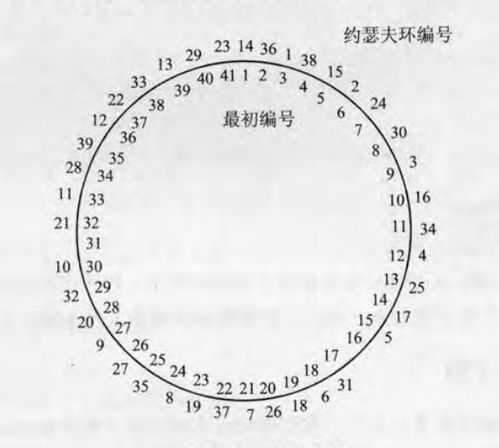
约瑟夫环问题可以描述为：有n个人围成一圈，从第一个人开始报数，每次报到m的人将被淘汰出局，然后从下一个人开始重新报数，如此循环，直到最后只剩一个人为止。我们的目标是找出这个最后剩下的人的初始编号。

三、递归解法

递归解法是解决约瑟夫环问题的一种经典方法。其基本思想是将问题分解为更小的子问题，然后通过递归调用自身来解决这些子问题。

递归解法的核心在于递推关系式的建立。当只有一个人时，显然这个人是最后的幸存者，编号为0。对于n个人，我们可以假设在淘汰了第m个人之后，剩下的人的编号为J(n-1, k)。由于环形结构的特点，我们需要对编号进行调整，即J(n, k) = (J(n-1, k) k) % n。

递归解法的实现如下：

```python

def josephus_recursive(n, k):

if n == 1:

return 0

else:

return (josephus_recursive(n - 1, k) k) % n

四、动态规划解法

动态规划解法是另一种解决约瑟夫环问题的有效方法。它通过将问题分解为更小的子问题，并存储这些子问题的解，从而避免重复计算。

动态规划解法的核心在于状态转移方程的建立。对于n个人，我们可以定义状态dp[n]表示在n个人中，最后剩下的人的编号。根据递推关系式，我们可以得到状态转移方程：dp[n] = (dp[n-1] k) % n。

动态规划解法的实现如下：

```python

def josephus_dynamic(n, k):

dp = [0] (n 1)

for i in range(2, n 1):

dp[i] = (dp[i - 1] k) % i

return dp[n]

五、循环链表解法

循环链表解法是利用循环链表来模拟约瑟夫环问题的过程。通过不断删除链表中的节点，我们可以找到最后剩下的人的编号。

循环链表解法的实现如下：

```python

def josephus_linked_list(n, k):

head = ListNode(0)

prev = head

for i in range(1, n 1):

prev.next = ListNode(i)

prev = prev.next

prev.next = head 形成循环链表

cur = head

while cur.next != cur:

for _ in range(k - 1):

cur = cur.next

cur.next = cur.next.next

return cur.val

约瑟夫环问题是一个经典的数学与算法问题，它考验着我们的数学思维和编程能力。本文介绍了递归解法、动态规划解法和循环链表解法，这些方法各有优缺点，可以根据具体问题选择合适的方法。通过学习约瑟夫环问题，我们可以更好地理解递归、动态规划和链表等算法和数据结构。